골프스윙 연습 글을 쓰려고 삽도를 그리려다가 인체비율에 맞게 넣으려고 황금비율을 검색했다.
레오나르도 다빈치, 앵무조개 등 황금비율에 대한 이야기가 많이 있었다.
갑자기 궁금해서 앵무조개를 한번 따라 그려봤다. 오~ 엄청 신기했다.

황금비율은 피보나치 수와 비슷하다고 한다. 예전에도 들었던 얘기인데... 오늘에서야 제대로 알게 되었다. 블로그를 시작하면서 글을 써야 하니 더 깊게 파고들어야 했고, 예전에 알았던 지식을 지금에서야 이해하는 일이 종종있다. 관심의 차이인 것 같다. 그 때 파고들었다면 긴 세월동안 이미 알고 있었던 지식이었을 텐데... 어설프게 아는 지식으로 어설픈 인간이어 왔네... 쯧...
피보나치 수는 0, 1, 1, 2, 3, 5, 8, 13, 21... 와 같이 앞의 두 수의 합과 같다.
0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8.... 이 관계에 대한 비율이 점차적으로 황금비율인 1.618에 수렴한다는 것이다.
그냥 그런가보다 했었는데... 소라를 그려보니 알게 되었다.
황금비율인 0.618을 'G'라고 쓰고, G^3인 0.236을 그렸을 때 오무라드는 위치의 끝이 맞은편의 위치와 딱 맞아떨어졌고, 그 이유는 앞의 두 수인 G^2와 G^3의 합이 G^1와 같기 때문이라는 것을 확인했기 때문이었다. 오~ 당연했지만 신기했고 이 수들은 피보나치 수열이기도 했지만 황금비율인 G의 제곱근의 수열이라는 것도 알게되었다. 비율에 비율에 비율을 곱하니 당연히 제곱근의 수열일테지... ㅎㅎㅎ
황금비율은 자연에서도 찾을 수 있는데 위의 그림처럼 앵무조개의 껍데기나 나뭇잎, 솔방울 등 황금비율 수열과 비슷하게 나타난다고 한다. 꼭 같지는 않고 비스므리 하다고 한다. 사람도 꼭 같다면 모두가 같아서 재미없으니 기본적인 최적의 표본에 조금씩 변형을 주어 하나님이 만드셨겠지... ㅎ

황금비율은 '짧은 변 길이(A)와 긴 변 길이(A+B)의 비는 다음 도형의 짧은변 길이(B)와 긴 변 길이(A)의 비와 같다로 정의된다. 과거 컴퓨터가 없던 시절에는 이 무리수를 찾는 것이 하나의 기술이었던 것 같다. 소숫점 자릿수를 많이 계산한 사람이 기록에 남겨질 정도였던 것 같다. 그래서 난 컴퓨터로 한번 해봤다.
엑셀에서 데이터 - 가상분석 - 목표값 찾기 / 찾는 값은 G이기도 하지만 B(0.618)를 찾아봤다.
A=1로 가정했을 때 G = B+1이니까.
그리고 A=B*G 이므로
1+B = 1/B 이고, 엑셀에 들어갈 수식은 B*(B+1)이고,
찾는 값은 1로 하고 돌리면,
0.618269755452522이 나오고, 수식은 1.00052724595984으로 완벽하게 찾지 못한다.
아~ 쉽지 않구나...
인터넷을 찾아보니 정확한 값이 나온다. B=0.618033988768953
엑셀에 넣어보니 수식값이 정확히 1로 떨어진다.
내 컴퓨터는 슈퍼 컴퓨터가 아닌 것이 증명되었다.
위 식을 약간 변환해 보면,
(A+B)/A = A/B = 0.618 = G 이고,
A=B*G, A+B=G로 변환할 수 있으며,
A=1 으로 가정하면,
G=1/B로 가장 간단한 식으로 정의할 수 있었다.
단순히 G(1.618)은 B(0.618)의 역수이다.
하다보니 왠지 이 수들이 연관이 있는 것 같아서 서로를 이래저래 곱해 봤다.... 그냥... 해봤다.
피보나치 수열이라 앞의 두수를 더하면 다음수가 나오는 수열인데...
1. 앞의 수를 앞앞의 수로 나눠봤다.(2-3-1)
처음의 수를 어떻게 놓느냐에 따라 다르게 전개가 되었는데... 몇가지만 돌려봤다.
B/G >> 나온수/G >> 앞의 수/앞앞의 수=(나온수/G)/(B/G) >> 계속 반복으로 긁었다.
B/G = B^2
B^2/G = B^3
B^3 / B^2 = B
B / B^3 = 1/B^2 이므로 G^2
.....
B^2 >> B^3 >> B^1 >> G^2 >> G^3 >> G^1 >> B^2 >> B^3 >> B^1 >> G^2 >> G^3 ... 이 반복되었다.
왠지 사인파와 같은 느낌이라 그래프로 돌려보니, 반복 그래프가 나왔다.

2. 앞의 수를 앞앞의 수로 나눠봤다.(1-2-1)
이번에는 놓는 수를 조금 달리하고 1과 같이 정리했다.
B >> B/G=B^2 >> 앞의 수/앞앞의 수 B^2/B >> 계속 반복으로 긁었다.
B^1 >> B^2 >> B^1 >> G^1 >> G^2 >> G^1 >> B^1 >> B^2 >> B^1 >> G^1 >> G^2 >> G^1 ... 이 반복되었다.
그래프로 돌려보니, 역시 반복 그래프가 나왔다. 아까보다는 크기가 조금 작은 그래프였다.

3. 앞의 수를 앞앞앞의 수로 나눠봤다.(증폭)
이번에는 G >> 1 >> B >> 앞의 수/앞앞의 수 B/G >> (B/G)/1 >> 계속 반복으로 긁었다.
G^1 >> 1 >> B^1 >> B^2 >> B^2 >> B^1 >> G^1 >> G^3 >> G^4 >> G^3 >> 1 ...
이번에는 제곱근이 반복하지 않고 진자로 움직이되 점점 커졌다.

수학은 재밋는 것 같다.
괜히 깊게 들어가서 시간가는줄 모르고 ... 많이 지나갔네... ㅠㅠ
찾다가 보니 3월 14일은 화이트 데이 이기도 하지만 원주율의 날이라는 것도 알았다.
파이=3.14니까.. ㅎㅎ
다음은 원주율을 한번 파봐야 겠다.
무리수로 시리즈를 엮어서.. ㅎㅎ
EBS 다큐프라임 - 세상을 바꾼 5개의 수 <넘버스>라는 것이 있는 것도 알아냈다.
꼭 보고 리뷰를 써야겠다.
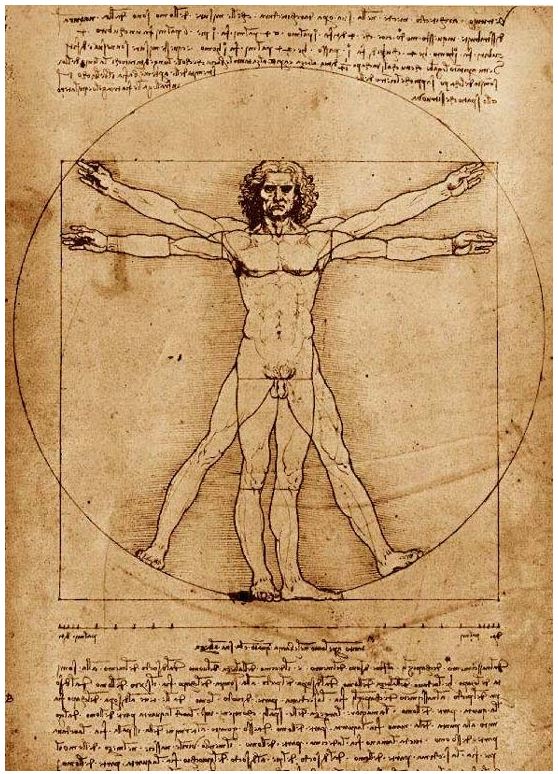
원래 이 그림으로 한번 해보려고 했는데...
'자연이 낸 인체의 중심은 배꼽이다.
등을 대고 누워서 팔 다리를 뻗은 다음 캠퍼스 중심을 배꼽에 맞추고 원을 돌리면
두 팔의 손가락 끝과 두발의 바가락 끝이 원에 붙는다.
정사각형으로도 된다.
사람 키를 발바닥에서 정수리까지 잰 길이는 두팔을 가로 벌린 너비와 같기 때문이다.'
우리나라의 도량형도 인체의 길이로 만들었다고 하니 이 것도 한번 찾아보고 정리해 봐야겠다.
'알쓸*잡' 카테고리의 다른 글
| 다수공급자 계약 개정(안) (0) | 2023.03.10 |
|---|---|
| 혁신제품이 좋은 이유 (0) | 2023.03.06 |
| 공공조달 혁신, 우수조달물품 규정 개정 (0) | 2023.03.02 |
| 2022 연말정산 수박 겉핥기 (0) | 2023.02.03 |
| 자주쓰는 강재 재질 비교(ASTM A36, A709 GR36, A709 GR50, SS275, SM355) (0) | 2022.09.27 |




댓글